Problem
The "key exchange problem" is encountered when 2 parties ("Alice" and "Bob") wish to communicate securely over an open, un-trusted network. Each can encrypt a message, but how can the password be exchanged securely without being physically together? What if Alice and Bob live in different countries? What if Alice is an internet banking customer, and Bob is a bank? Historically, passwords and secret keys were exchanged by courier, people who would carry the password between the parties wishing to communicate.
Whitfield Diffie and Martin Hellman (and Ralph Merkle) devised a mathematical solution to the key exchange problem. Their method, Diffie-Hellman (D-H) Key Exchange, enables 2 parties to establish a shared secret (password) without the need to be physically in the same location.
Read the Wikipedia page.
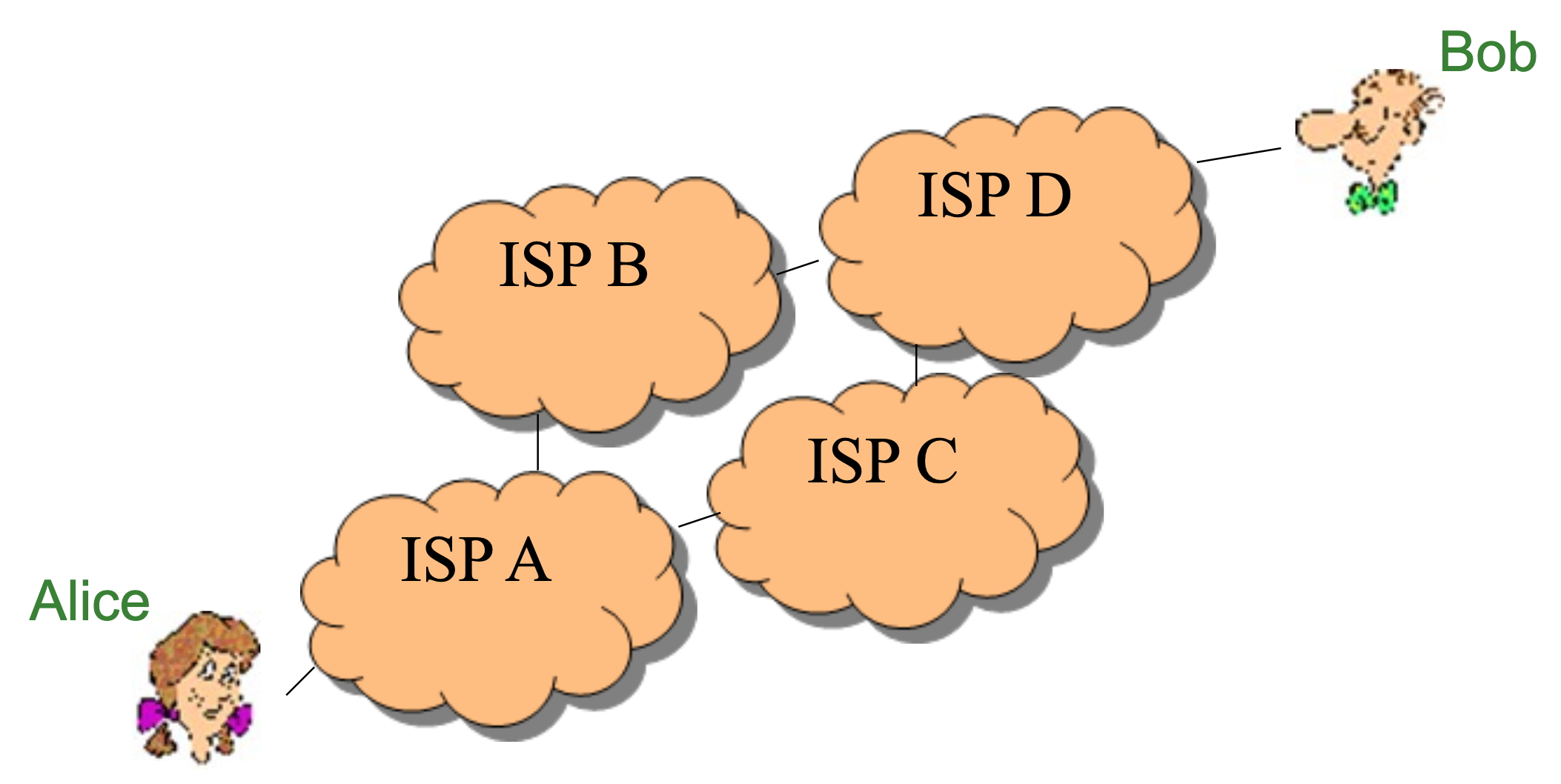
How would you solve the key exchange problem?
The Math
Let us practice some of the mathematics that are used in the D-H protocol.
The 'mod' operator performs division and then gives the remainder. The 'mod' operator often is expressed with the '%' symbol. The use of a calculator with these problems is permitted, however, they are simple enough to be done by hand with paper and pencil.
44 mod 6 = 27 % 7 = 8 mod 3 = 100 % 10 = 1000000 mod 10 = 11 % 10 = 1000001 mod 10 = 31415927 % 7 = 3 mod 2 = 1234567890123456789 % 2 =
Here we have base ^ exponent % prime.
Raising a base to an exponential power is a calculation that is easy for a computer. Finding the modulus of a number is simple for a computer. Even when the numbers involved are very large, computers can perform the calculations directly. However, finding the exponent given the base and the modulus is difficult. Mathematicians call it hard. This means that brute force is required, and when the numbers are large, the solution cannot be found in any reasonable amount of time.
Solve each of the below equations for N or declare the solution hard.
2 ^ 3 mod 5 = N 5 ^ 2 % 13 = N 2 ^ 17 mod 37 = N 5 ^ 8 % 97 = N 5 ^ N mod 87 = 16 3 ^ N % 53 = 30 7 ^ 8 mod 3891 = N 5 ^ 123456 % 3891 = 2959 5 ^ 1234567 % 3891 = 3674
Conceptual Idea
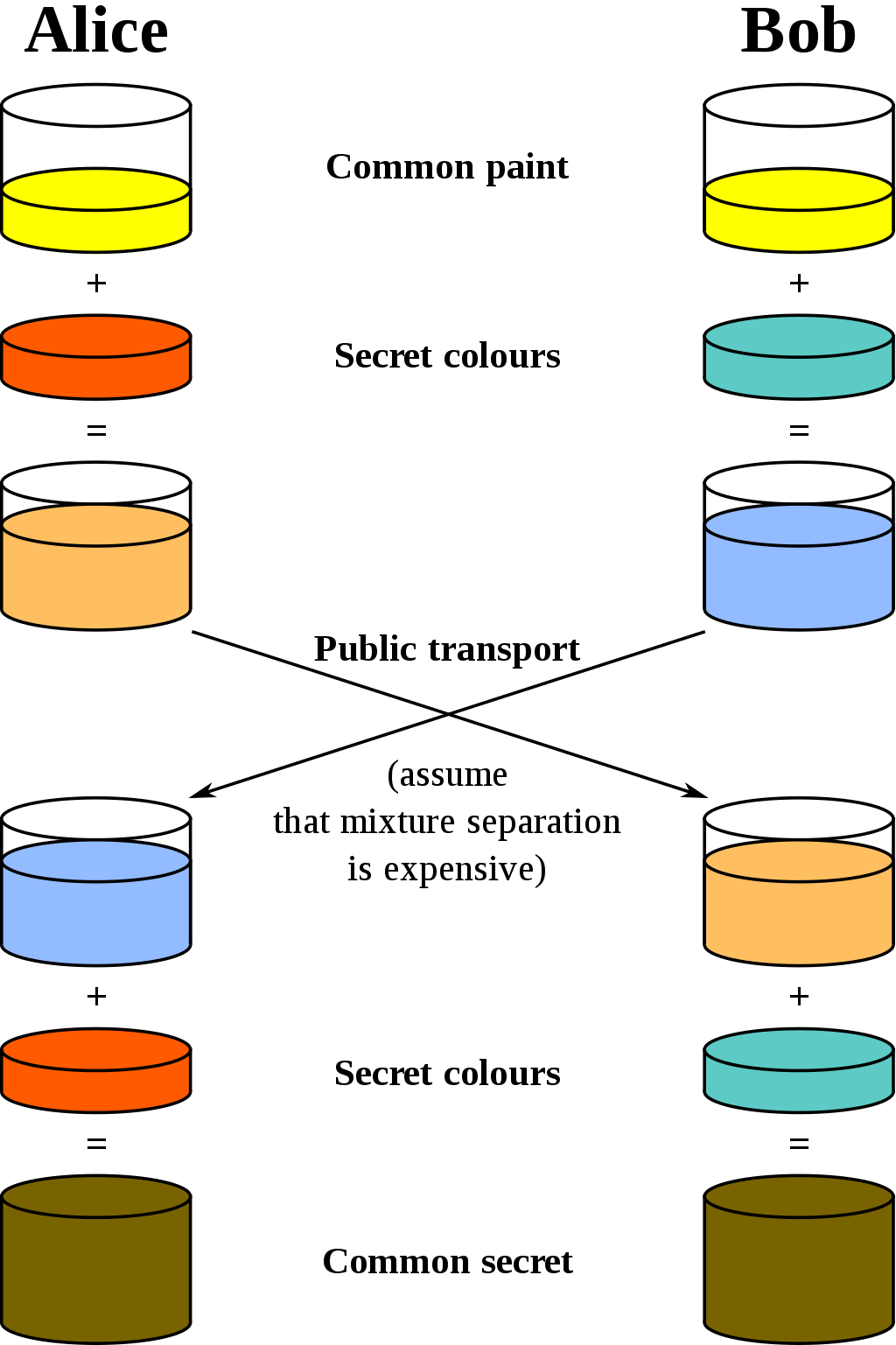
Below is a conceptual image of what D-H will do. Two people start with a common paint. We will call the common color 'g_P'.
Alice has a secret color called 'a'. Bob has a secret color called 'b'.
Alice mixes the shared color with her secret color to get 'A'. Bob mixes the shared color with his secret color to get 'B'.
Alice sends her 'A' mixture to Bob; Bob sends his 'B' mixture to Alice.
Alice mixes her secret color 'a' with Bob’s mixture color 'B' and gets 'K'. Bob mixes his secret color 'b' with Alics’s mixture color 'A' and gets 'K'.
'K' and 'K' are the same!
Examples and Exercises
Perform a full Diffie-Hellman key exchange for the following sets of starting points. Assume a base of g and modulus of p. Alice’s private key is a; Bob’s private key is b. Solve for Alice’s public key, Bob’s public key and the shared secret A, B and K respectively. (Show your work if you desire any partial credit.)
Work Matrix
The following is the work matrix.
| Alice | Bob |
|---|---|
g ^ a mod P = A |
g ^ b mod P = B |
B ^ a mod P = K_Ba |
A ^ b mod P = K_Ab |
Diffie-Hellman Procedure
-
(Alice) Fill in g, a, P to calculate A.
-
(Bob) Fill in g, b, P to calculate B.
-
Exchange A and B. (Alice sends A to Bob; Bob sends B to Alice.)
-
(Alice) Fill in B, a, P to calculate K_Ba.
-
(Bob) Fill in A, b, P to calculate K_Ab.
-
Ensure that K_Ba and K_Ab match.
Walk Through with Alice and SpongeBob
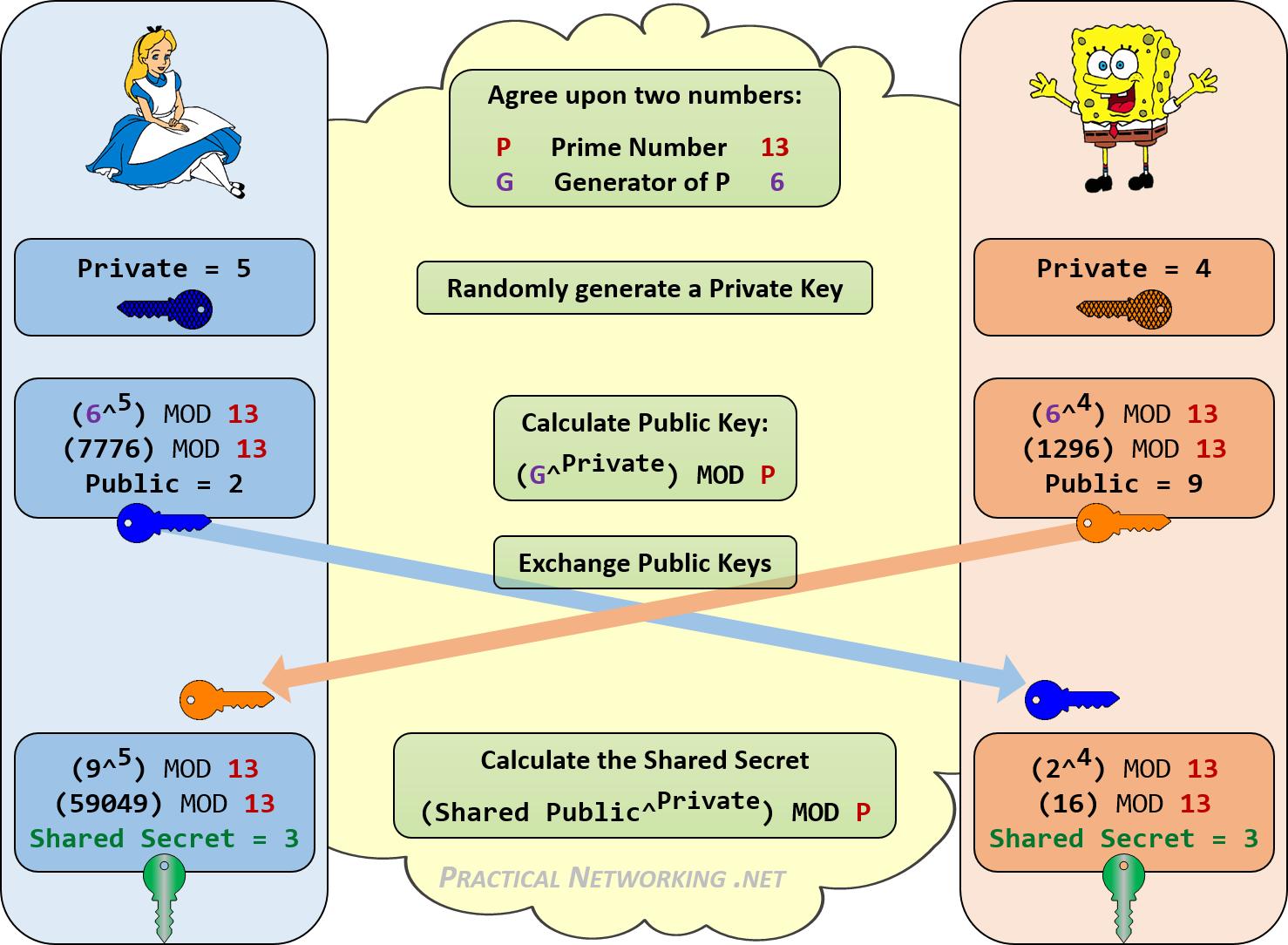
Example 1
The following is an example worked out for you.
| Alice | Bob |
|---|---|
5 ^ 2 % 19 = A = 6 |
5 ^ 5 % 19 = B = 9 |
9 ^ 2 % 19 = K_Ba = 5 |
6 ^ 5 % 19 = K_Ab = 5 |
5 == |
== 5 |
Example 2
g = 2, p = 11, a = 7, b = 3
Example 3
g = 7, p = 3081, a = 47, b = 31
Example 4
g = 2, p = 11, a = 3, b = 5
Another D-H Diagram
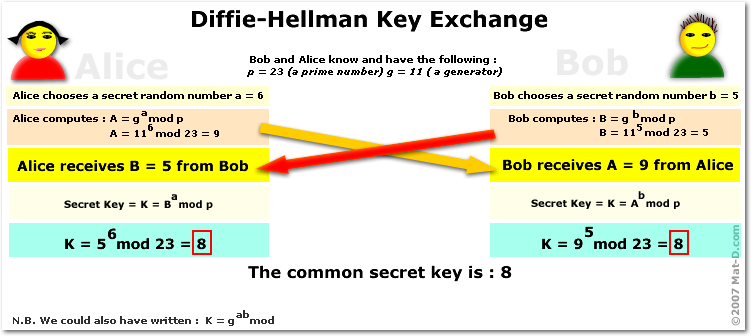
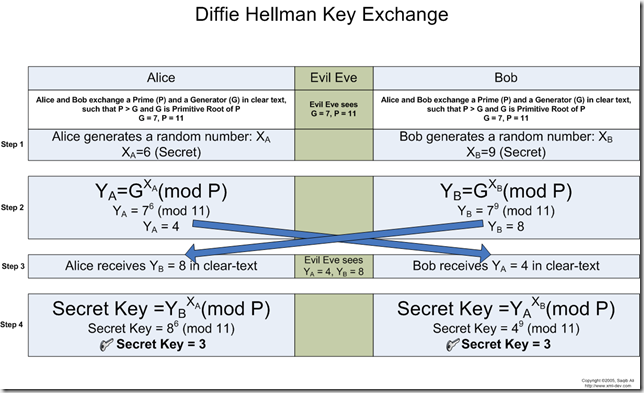
D-H with Eve the Eavesdropper
In this example, Eve is illustrated listening to the in-between exchanges.
Another D-H Diagram
